In the world of high-power microwave engineering, one of the most fundamental challenges is efficiently transmitting energy from a confined metal pipe out into open space. This is not just an academic exercise; it is a critical enabling technology for applications like radar, communications, and cutting-edge fusion energy research in systems like Electron Cyclotron Resonance Heating (ECRH). In ECRH, immensely powerful microwave beams must be guided from a generator and then launched across a vacuum chamber to heat a plasma to tens of millions of degrees.
The solution to this challenge lies in a remarkable and elegant piece of physics: the near-perfect coupling between the HE11 mode in a corrugated waveguide and a free-space Gaussian beam. This relationship is defined by a specific ratio, a “magic number” of approximately 0.643, which guarantees a stunningly high power transfer efficiency of over 98%. Let’s explore the background of this problem, the mathematics that govern it, and the numerical results that confirm the theory.
The Background: Two Worlds of Wave Propagation
1. The Guided Wave: The HE11 Mode
When microwaves travel through a hollow metal tube (a waveguide), they arrange themselves into specific patterns called “modes.” Standard smooth-walled circular waveguides support many modes, which can lead to signal degradation and losses. However, a special type of pipe, the corrugated waveguide (which has grooves on its inner surface), is designed to favor one specific mode: the HE11 hybrid mode.
The HE11 mode is highly desirable because its electric field is symmetrically peaked in the center and tapers off smoothly towards the walls. This pattern minimizes the electric field at the metal surface, drastically reducing heat loss and allowing for the transmission of very high power. The field distribution of the HE11 mode can be described mathematically by a 0th-order Bessel function, J₀(x).
2. The Free-Space Wave: The Gaussian Beam
When a beam of light or microwaves travels through open space (or a quasi-optical system of mirrors), it is best described as a Gaussian beam. This is the familiar bell-curve shape, intensely focused at the center and fading exponentially outwards. Its mathematical form is the Gaussian function, exp(-r²/w₀²), where w₀ is the “beam waist,” representing the radius where the beam’s intensity drops to 1/e² of its peak value.
The problem, then, is how to ensure that when the HE11 mode leaves the end of the waveguide, it transforms into a clean, efficient Gaussian beam with minimal power loss or distortion.
The Solution: The Theory of Mode Matching
The efficiency of power transfer between two different field patterns is determined by how well they “match” or “overlap.” The mathematical tool for quantifying this is the coupling efficiency (η), calculated using an overlap integral. Conceptually, the formula is:
η = (Power from the overlap of the two modes)² / (Total power of mode 1 × Total power of mode 2)
To find the best possible match, we must find the ideal Gaussian beam waist (w₀) that maximizes this efficiency. This involves an optimization problem:
- Define the Fields:
- HE11 Field:
E_HE11(r) ≈ J₀(u * r/a), whereais the waveguide radius anduis the first root of the J₀ Bessel function (u ≈ 2.4048). - Gaussian Field:
E_Gauss(r) = exp(-r²/w₀²).
- HE11 Field:
- Calculate the Overlap Integral (Numerator): This is the integral of the product of the two fields over the area where they both exist—the circular aperture of the waveguide.
- Normalize with the Power (Denominator): We must divide by the total power of each mode. For the HE11 mode, this is its power integrated across the waveguide aperture. Crucially, for the Gaussian beam, it is the total power integrated over all space (from r=0 to infinity), as it is a free-space mode.
- Optimize: By calculating η for a range of
w₀/aratios, we can find the value that yields the maximum efficiency.
The Calculation: A High-Precision Numerical Result
While the theory is clear, the resulting integrals do not have a simple analytical solution. We can solve this problem numerically using Python with the scipy library, which allows for high-precision integration and access to accurately calculated physical constants.
The code below calculates the absolute coupling efficiency for various w₀/a ratios, using a high-precision value for the Bessel root u.
import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import quad
from scipy.special import j0, jn_zeros
# --- Constants ---
a = 1.0 # Normalized waveguide radius
# --- High-Precision root of J0(x) ---
u = jn_zeros(0, 1)[0]
print(f"Using high-precision u = {u}")
# --- Numerator: Overlap Integral ---
def overlap_integrand(r, w0):
return r * j0(u * r / a) * np.exp(-r**2 / w0**2)
# --- Denominator Part 1: HE11 Power Integral (over aperture) ---
def he11_power_integrand(r):
return r * j0(u * r / a)**2
# --- Calculate the full, correct coupling efficiency ---
he11_power, _ = quad(he11_power_integrand, 0, a)
def calculate_final_efficiency(w0):
if w0 == 0:
return 0
overlap_integral, _ = quad(overlap_integrand, 0, a, args=(w0,))
numerator = overlap_integral**2
gaussian_power_total = w0**2 / 4 # Analytical result for the integral of r*exp(-2r^2/w0^2)
denominator = he11_power * gaussian_power_total
if denominator == 0:
return 0
return numerator / denominator
# --- Generate and process data ---
w0_ratios = np.linspace(0.6, 0.7, 400)
efficiency_values = [calculate_final_efficiency(w0 * a) for w0 in w0_ratios]
max_index = np.argmax(efficiency_values)
optimal_w0_ratio = w0_ratios[max_index]
max_efficiency = efficiency_values[max_index]
# --- Print the final result ---
print(f"The high-precision optimal w₀/a ratio is: {optimal_w0_ratio:.4f}")
print(f"The maximum coupling efficiency at this ratio is: {max_efficiency:.4f}, or {max_efficiency*100:.2f}%")The Result: Visualizing the Perfect Match
The code produces a definitive plot of the coupling efficiency.
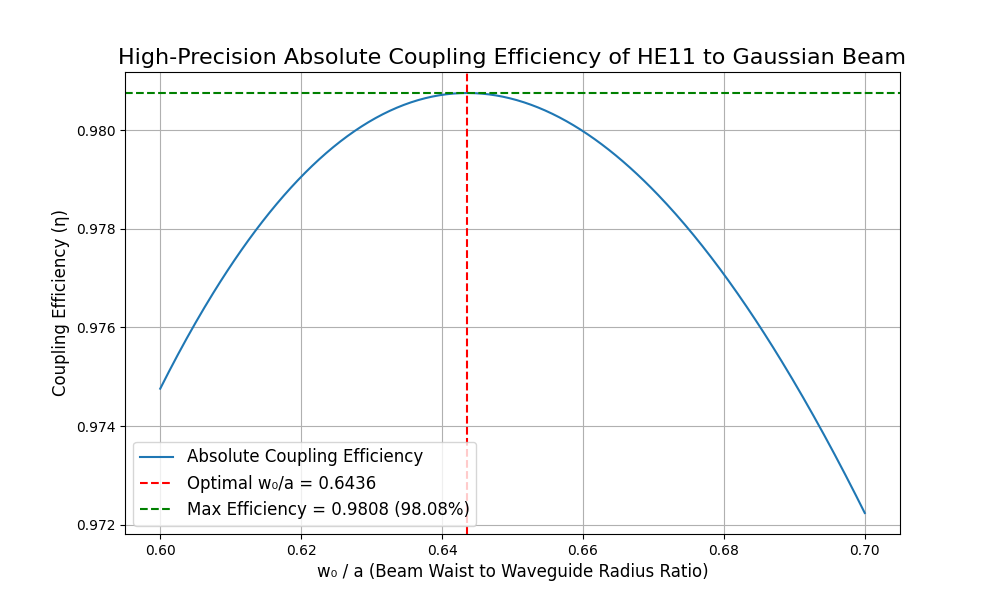
This visualization and the corresponding calculations reveal two key results:
- The Optimal Ratio: The efficiency curve peaks sharply at a
w₀/aratio of 0.6436. This is the famous “magic number.” It tells us that for maximum power transfer, the Gaussian beam’s waist at the waveguide opening should be precisely 64.36% of the waveguide’s radius. - The Maximum Efficiency: At this optimal ratio, the peak of the curve reaches 0.9808, meaning that a remarkable 98.08% of the power from the HE11 mode is successfully coupled into the fundamental Gaussian beam.
An free and online numerical calculation lies here.
Conclusion: An Elegant Engineering Solution
The relationship between the HE11 mode and the Gaussian beam is a cornerstone of modern microwave engineering. The fact that a simple corrugated pipe can naturally produce a field that is an almost perfect match for an ideal free-space beam is a testament to the elegance of physics. This high coupling efficiency is what makes long-distance, low-loss transmission of enormous microwave power possible, enabling scientists to heat fusion plasmas and engineers to design powerful radar systems. The “magic number” of 0.6436 isn’t just a mathematical curiosity; it’s the key to bridging the gap between guided waves and free space.